Aggiornato il 6 Maggio 2025
L’affascinante storia della mela caduta in testa a Isaac Newton durante una visita alla madre intorno al 1666 diffusa per la prima volta da John Conduitt è probabilmente una sintesi romanzata di un processo più complesso che portò il fisico britannico a elaborare la legge di gravitazione universale tra il 1665 e il 1666. Questa storia, però, citata con i dubbi opportuni sulla sua veridicità , può diventare un ottimo punto di partenza per verificare con uno stile alla Fermi la plausibilità della scoperta di Newton.
Partiamo dalla Luna: il suo periodo orbitale risulta \(2.4 \cdot 10^6 \, s\), mentre il raggio della sua orbita è \(3.8 \cdot 10^8 \, m\). Di conseguenza la sua accelerazione centripeta è
\[a_c = \left ( \frac{2\pi}{T} \right )^2 r \approx 2.6 \cdot 10^{-3} \, m \, s^{-2}\]
D’altra parte una mela o un qualunque oggetto in caduta libera sulla superficie della Terra possiede un’accelerazione pari a \(9.8 \, m \, s^{-2}\). Se confrontiamo queste due accelerazioni, scopriamo che il loro rapporto è pari circa a \(2.8 \cdot 10^{-4}\). Un rapporto molto simile si riscontra tra i quadrati del raggio della Terra e del raggio orbitale della Luna, che è all’incirca 60 volte quello della Terra:
\[\frac{R^2}{r^2} = \frac{1}{3600} \approx 2.8 \cdot 10^{-4}\]
Quindi si è naturalmente portati a generalizzare come segue:
\[\frac{a_c}{g} = \frac{R^2}{r^2}\]
da cui
\[a_c r^2 = g R^2 = C\]
con \(C\) costante reale.
La forza centripeta sulla Luna in orbita intorno alla Terra sarà allora data dall’espressione
\[F = m a_c = m g \frac{R^2}{r^2} = \frac{mC}{r^2}\]
Per la legge dell’azione e reazione (la terza legge della dinamica di Newton), questa forza è in modulo uguale alla forza esercitata dalla Terra sulla Luna, quindi la costante \(C\) deve essere proporzionale alla massa \(M\) della Terra, ovvero qualcosa del tipo \(C=GM\), con \(G\) costante di gravitazione universale.
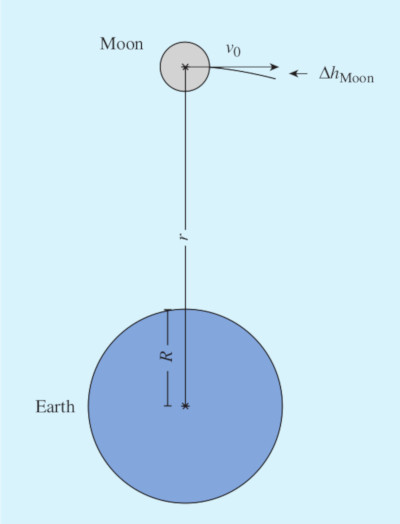 Andiamo alla mela e proviamo a confrontare la sua caduta vicino alla superficie della Terra con la caduta della Luna. Per fare ciò prendiamo in considerazione un intervallo di tempo sufficientemente piccolo rispetto al periodo orbitale della Luna in modo tale da poter approssimare l’arco di circonferenza percorso dal nostro satellite con una traiettoria rettilinea percorsa da un proiettile in un campo gravitazionale.
Andiamo alla mela e proviamo a confrontare la sua caduta vicino alla superficie della Terra con la caduta della Luna. Per fare ciò prendiamo in considerazione un intervallo di tempo sufficientemente piccolo rispetto al periodo orbitale della Luna in modo tale da poter approssimare l’arco di circonferenza percorso dal nostro satellite con una traiettoria rettilinea percorsa da un proiettile in un campo gravitazionale.
In questo caso avremo che
\[\Delta t = \frac{\Delta s}{v_0}\]
dove \(\Delta t\) è l’intervallo di tempo considerato, \(\Delta s\) la lunghezza dell’arco, \(v_0 = 2\pi r/T\) è l’intensità della velocità orbitale.
Se supponiamo che la componente radiale della velocità orbitale è nulla, allora la variazione di altezza di caduta della Luna verso la Terra sarà data dall’espressione
\[\Delta h_{\text{Luna}} = \frac{a_{\text{Luna}}}{2} \left ( \frac{\Delta s}{v_0} \right )^2\]
con \(a_{\text{Luna}}\) l’accelerazione centripeta della Luna. Quest’ultima, utilizzando i dati forniti all’inizio, risulta pari a:
\[a_{\text{Luna}} = \left ( \frac{2\pi}{T} \right )^2 r \approx 2.6 \cdot 10^{-3} \, m \, s^{-2}\]
Nel frattempo una mela in caduta nello stesso intervallo di tempo ha una variazione di quota pari
\[\Delta h_{\text{mela}} = \frac{g}{2} \left ( \frac{\Delta s}{v_0} \right )^2\]
Se confrontiamo le due variazioni otteniamo un interessante risultato:
\[\frac{\Delta h_{\text{Luna}}}{\Delta h_{\text{mela}}} = \frac{a_{\text{Luna}}}{g} \approx 2.7 \cdot 10^{-4}\]
che è molto simile ai rapporti precedentemente calcolati, in particolare quello tra i quadrati dei raggi.
Da questo risultato possiamo concludere che: innanzitutto che non è implausibile paragonare la caduta di un oggetto verso la superficie della Terra con il moto della Luna intorno al nostro pianeta e soprattutto che la forza che lega la Luna alla Terra è inversamente proporzionale al quadrato della distanza.
Supponiamo, infine, che il nostro satellite si trovi a cadere sulla Terra da un’altezza prossima alla superficie del pianeta. Potremmo stimare la sua accelerazione di caduta a partire dalla relazione:
\[\frac{a’_{\text{Luna}}}{a} = \frac{r^2}{R^2} = 3600\]
da cui
\[a’_{\text{Luna}} = 3600 \cdot a \approx 9.4 \, m \, s^{-2}\]
che non è molto distante dal valore dell’accelerazione di gravità terrestre.



Add Comment