Aggiornato il 5 Giugno 2025
Uno degli esperimenti più classici con il quale misurare l’accelerazione di gravità , realizzabile anche in un laboratorio di fisica di una qualsiasi scuola superiore, è mettendo in oscillazione un pendolo semplice. Le misure chiave in un esperimento di tal genere sono quelle sulla lunghezza del filo del pendolo e sul tempo di oscillazione. Se la prima misura può essere realizzata senza troppi problemi con un semplice righello, la misura sul periodo di oscillazione risulta più complicata dovendo valutare il punto massimo e il punto minimo dell’oscillazione del pendolo e viene usualmente realizzata da ciascun componente del gruppo di studenti, anche più di una volta a studente. Tale operazione, però, può essere semplificata utilizzando i sensori di cui sono dotati gli smartphone, ormai sempre più diffusi sia tra gli insegnanti sia tra gli studenti.
Gli smartphone nel laboratorio di fisica
Molti esperimenti di fisica possono essere oggi realizzati con relativa semplicità grazie ai sensori di cui sono dotati gli smartphone, installando le applicazioni opportune per la raccolta e la visualizzazione dei dati.
Tra gli esperimenti che si possono realizzare si contano lo studio della caduta libera usando l’accelerometro; lo studio del moto armonico; la misura della velocità e dell’accelerazione di un oggetto che emette luce; la misura del campo magnetico generato da una carica in movimento; l’utilizzo dell’effetto Doppler per studiare il moto lineare; lo studio delle proprietà acustiche e meccaniche di una corda vibrante.
Nel caso della proposta che vi andremo a raccontare a breve, utilizzando il sensore luminoso dello smartphone sarà possibile misurare il tempo di oscillazione di un pendolo e quindi misurare l’accelerazione di gravità corrispondente alla propria latitudine.
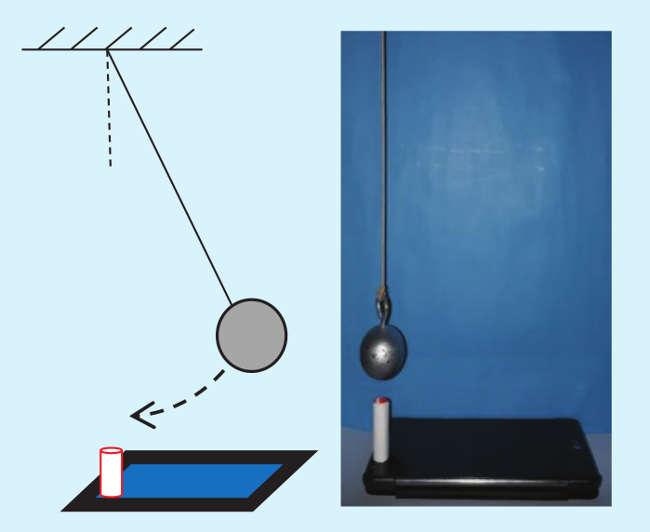
Le oscillazioni del pendolo
Il pendolo semplice è un dispositivo costituito da un filo e da un peso attaccato. Messo in oscillazione a piccoli angoli, ha la proprietà di mantenere un periodo di oscillazione pressochè costante. Esso risulta essere pari a:
\(T = 2 \pi \sqrt{\frac{L}{g}}\)
dove \(T\) è il periodo di oscillazione, \(L\) la lunghezza del pendolo, \(g\) l’accelerazione di gravità .
Questa può essere facilmente linearizzabile elevando al quadrato ambo i membri dell’equazione:
\(T^2 = \frac{4 \pi^2}{g} L\)
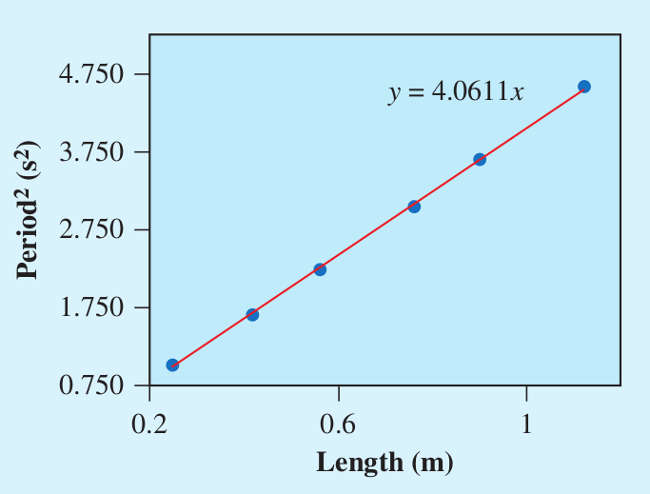
àˆ facile osservare a questo punto che ponendo \(T^2\) come \(y\) ed \(L\) come \(x\) il grafico risultante sarà una retta il cui coefficiente angolare sarà pari a:
\(m = \frac{4 \pi^2}{g}\)
L’obiettivo dell’esperimento sarà allora misurare il periodo di oscillazione del pendolo semplice per differenti lunghezze (almeno sei) e utilizzando la propagazione degli errori, o gli strumenti di calcolo automatici messi a disposizione dal foglio di calcolo utilizzato, determinare la misura dell’accelerazione di gravità con il suo errore. Il valore ottenuto andrà quindi confrontato con il valore corrispondente alla latitudine dell’esperimento.
Raccolta ed elaborazione dei dati
Il set-up sperimentale è abbastanza semplice: uno smartphone, un foglietto di carta (o di altro materiale) arrotolato a cilindro da incollare sulla fotocamera, un pendolo, un’applicazione di gestione dei sensori del telefono a scopo sperimentale/educativo come ad esempio Physics Toolbox Suite.
Si pone il pendolo in posizione di riposo esattamente sopra il cilindro di carta (lo si utilizza per ridurre al minimo il fondo luminoso), si fa partire il misuratore di intensità luminosa (luxmetro) e la raccolta dei dati, quindi si mette il pendolo in oscillazione. Dopo una decina di oscillazioni (o poco più) si può interrompere la raccolta dati, che verranno estratti in formato .csv e quindi leggibili da qualsiasi foglio elettronico (anche on-line).
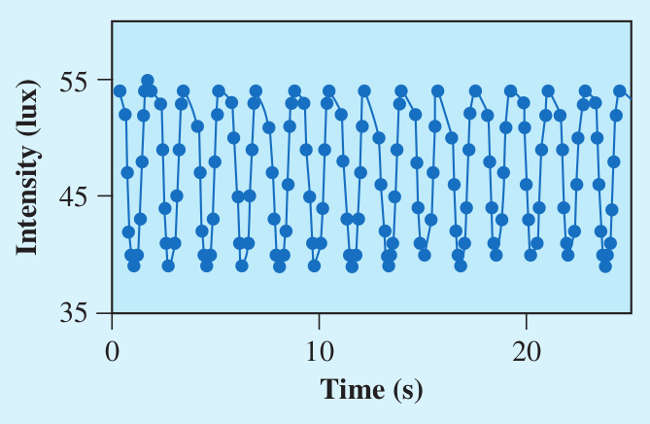
Il grafico ottenuto risulterà periodico e il periodo coincidente con la distanza temporale tra due picchi o due valli. Ovviamente per determinare il periodo di oscillazione del pendolo, sarà utile fare la media tra tutte le distanze temporali picco-picco o valle-valle.
Con i dati così raccolti ed elaborati, si realizzerà un grafico \(T^2\)–\(L\), la cui pendenza risulta legata all’accelerazione di gravità . Il risultato finale va confrontato con il valore locale, che può essere determinato a partire dalla formula fornita dal National Physical Laboratory britannico.



Add Comment