Chi dimostrò che la Terra era tonda?

Aggiornato il 28 Novembre 2024

Si dice che già  gli antichi Greci (e fra questi Eratostene) avessero dimostrato che la Terra non era piatta, ma aveva una forma che si assumeva sferica. Ma la questione non è così chiara come la si racconta.
Nell’epoca pre-socratica, la maggior parte dei filosofi greci si atteneva al modello della Terra piatta; per esempio, il celebre Talete da Mileto considerava le terre emerse come un disco piatto che galleggiava sull’acqua. Il primo a mettere in discussione questo modello fu Anassimandro, che considerava la Terra come un tozzo cilindro fluttuante nello spazio di altezza uguale a un terzo del raggio, dove tutte le terre emerse si trovavano sulla base superiore.
Non esistono purtroppo resoconti scritti di come la sfericità  della Terra sia stata dimostrata e le ricostruzioni degli esperti non sono riusciti ad attribuire con certezza la paternità  dell’idea. Secondo alcuni autori, il primo a pronunciarsi in proposito fu Pitagora, verso il 500 a.C.: osservando la forma del terminatore lunare, ossia della linea che separa luce e ombra sulla Luna, dedusse che il nostro satellite dovesse avere forma sferica, e gli sembrò logico supporre che Terra e Luna avessero la stessa forma. Secondo altri studiosi, le idee di sfericità  della Terra erano note già  ad altri filosofi come Parmenide.

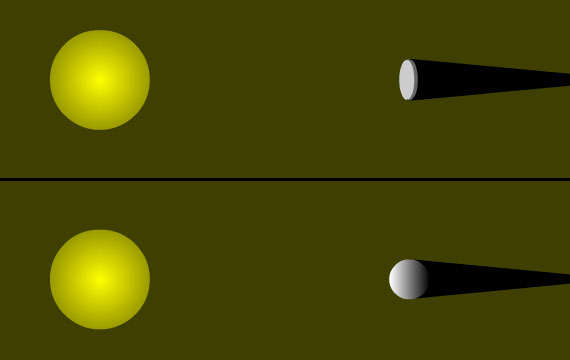
Tra il 500 e il 430 a.C., Anassagora determinò che la causa delle eclissi lunari era l’ombra della Terra. Poichè l’ombra era sempre rotonda, anche in questo caso sembrò logico dedurne una forma terrestre sferica. Certo, teoricamente anche una Terra a forma di disco piatto potrebbe gettare un’onda circolare sulla Luna, ma dovrebbe essere sempre orientata nello stesso modo; un’ipotesi simile sembrava una forzatura non necessaria.

Un’ulteriore osservazione a sostegno della teoria di una Terra sferica venne da Aristotele, che nel 350 a.C. notò come alcune costellazioni visibili dall’Egitto scomparissero sotto l’orizzonte se si osservava il cielo dall’Europa, e viceversa. Ad Aristotele si fa anche risalire il famoso argomento della nave, per il quale la curvatura terrestre fa sì che di una nave in arrivo si vedano prima le vele, poi la prua e infine la poppa (e viceversa per una nave in partenza). Tuttavia, la prima testimonianza di questo argomento la si trova solo negli scritti di Plinio il Vecchio, nel 77 d.C., ossia più di quattro secoli dopo.

Non è raro leggere che fu Eratostene da Cirene a dimostrare che la Terra fosse sferica misurandone il raggio, ma anche questa, se vogliamo essere precisi, è un’affermazione impropria. Come abbiamo visto, all’epoca di Eratostene (III Secolo a.C.) la sfericità  della Terra si considerava assodata non tanto in virtù di una dimostrazione matematica, ma a seguito di una serie di osservazioni che l’ipotesi di una Terra sferica spiegava nel modo più semplice e naturale.
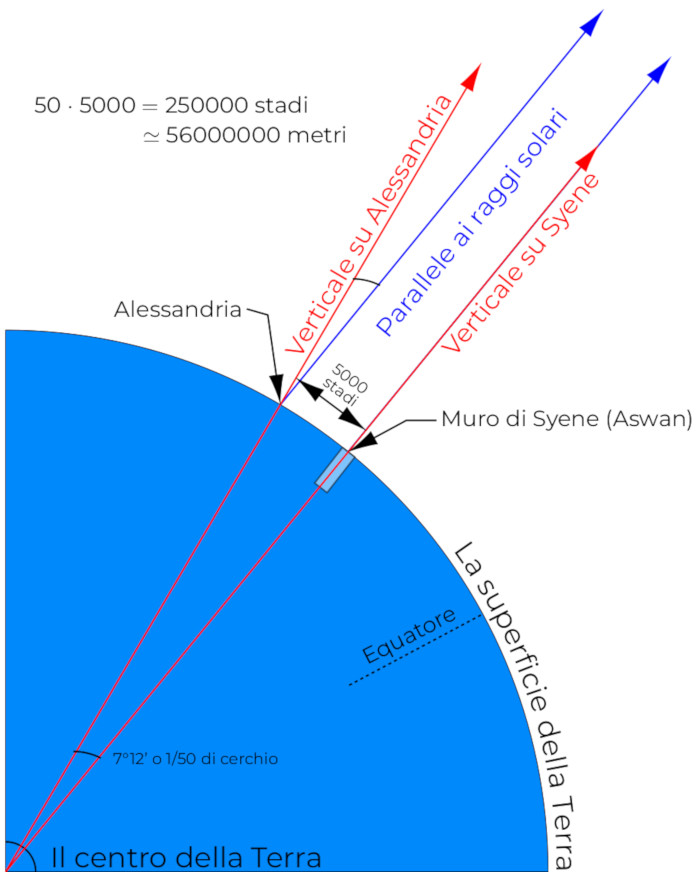
Infatti, quello che fece Eratostene fu di assumere che la Terra fosse sferica come ipotesi, e che il Sole fosse abbastanza lontano da considerare in suoi raggi come paralleli. Eratostene notò che nella città  di Siene, l’attuale Assuan, quando il Sole si trovava allo zenit (cioè nel punto più alto del suo percorso apparente nel cielo) non gettava ombre: questo perchè Assuan si trova nei pressi del tropico del Cancro dove, a causa dell’inclinazione terrestre, i raggi solari cadono perpendicolarmente al terreno nel solstizio d’estate. Invece, nello stesso periodo, nella città  di Alessandria l’ombra era inclinata di 1/50 di angolo giro, ossia circa 12 gradi 7 gradi e 12 primi⁽¹⁾Un grazie al nostro lettore Alessio Gennari per la segnalazione della svista – NdR. Eratostene misurò la distanza tra Siene e Alessandria che risultò essere di 5000 stadi.
Con le ipotesi menzionate in precedenza e tramite una semplice proporzione, Eratostene calcolò la circonferenza terrestre stabilendo una lunghezza di 252.000 stadi, ossia un valore compreso tra 39.690 a 46.620 km a seconda del tipo di stadio considerato; comunque una misura molto precisa per gli strumenti dell’epoca se confrontata con quella attuale di 40.075 km.

Come abbiamo visto, l’ipotesi di Terra sferica era considerata la più sensata, almeno dai filosofi di una qualche autorevolezza; si poteva dire lo stesso dell’ipotesi di un Sole estremamente lontano? L’astronomo Aristarco di Samo aveva già  tentato di stimare la distanza Terra-Sole, ma le sue misure erano molto imprecise (anche se, come si scoprì poi, l’aveva sottostimata di un fattore 20). Cosa succederebbe se, per assurdo, rifiutassimo entrambe le ipotesi adottate da Eratostene?
Ebbene, le sue misure potrebbero comunque essere riprodotte ipotizzando una Terra piatta e un Sole abbastanza vicino alla Terra da far sì che i suoi raggi non siano più paralleli. La situazione si può schematizzare con la seguente figura:

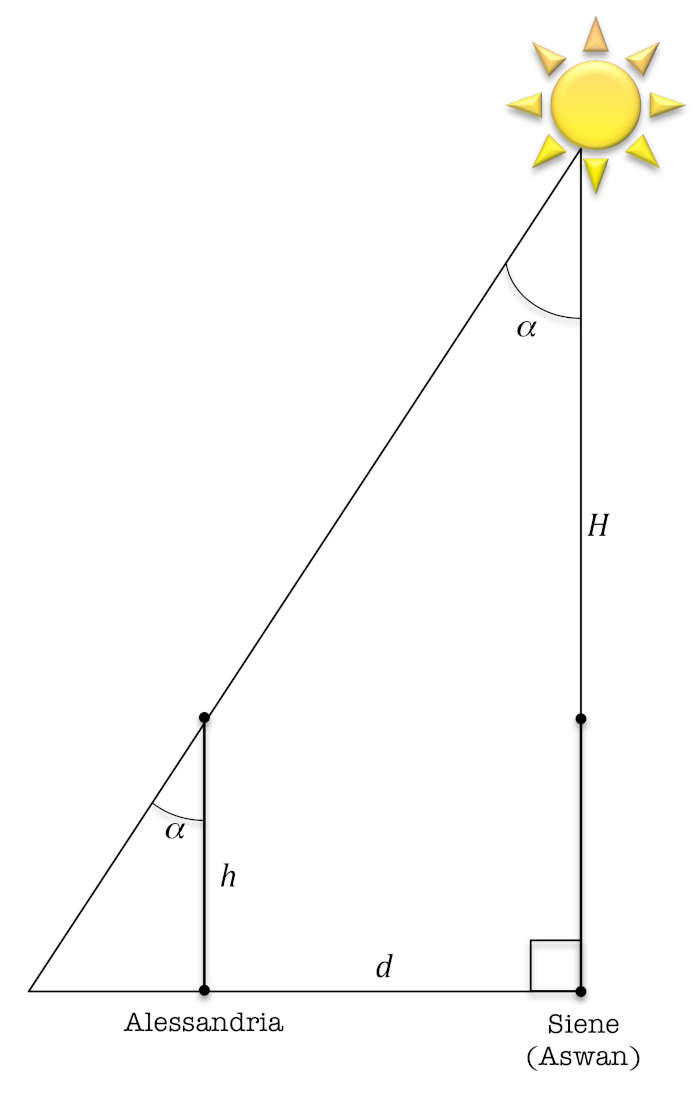
In questa figura, \(H\) è l’altezza del Sole, \(d\) è la distanza tra Siene e Alessandria, \(h\) è l’altezza di un oggetto di riferimento posto ad Alessandria e \(alpha\) è l’inclinazione dei raggi del Sole, sempre ad Alessandria.
Applicando le proporzioni ai triangoli simili e usando un po’ di trigonometria di base, si può dimostrare che i dati di Eratostene sono coerenti con una Terra piatta e un Sole che si trova alla distanza dalla Terra data da:

\[H = frac{d}{tan alpha} + h\]

Sostituendo i valori ottenuti da Eratostene per \(d\) e \(alpha\) e ipotizzando che \(h\) non superi un’altezza massima di qualche metro, si trova che il secondo addendo è trascurabile e quindi

\[H simeq frac{d}{tan alpha} simeq 6 div 8 km\]

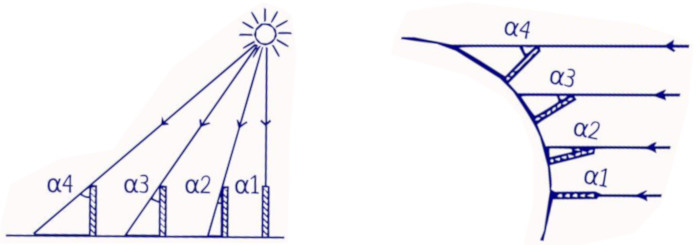
che è inferiore all’altezza delle nostre montagne più alte, ma più alto delle montagne note ai tempi dell’Antica Grecia. È comunque possibile ripetere l’esperimento di Eratostene da tre località  poste a latitudini diverse; in tal caso, ripetendo le misure e facendo le debite proporzioni, sarebbe possibile sciogliere il dubbio, e i risultati non sarebbero compatibili con un modello di Terra piatta.

Nel corso della storia successiva, numerose evidenze indipendenti andavano a corroborare l’idea di una Terra sferica, arrivando alla circumnavigazione del globo da parte di Magellano e alle foto satellitari del nostro pianeta. Che, a dirla tutta, non è proprio una sfera, essendo schiacciata ai poli a causa della rotazione sul suo asse… ma questa è un’altra storia!